Home » Full Forms » BODMAS: The key to basic mathematics
BODMAS: The key to basic mathematics
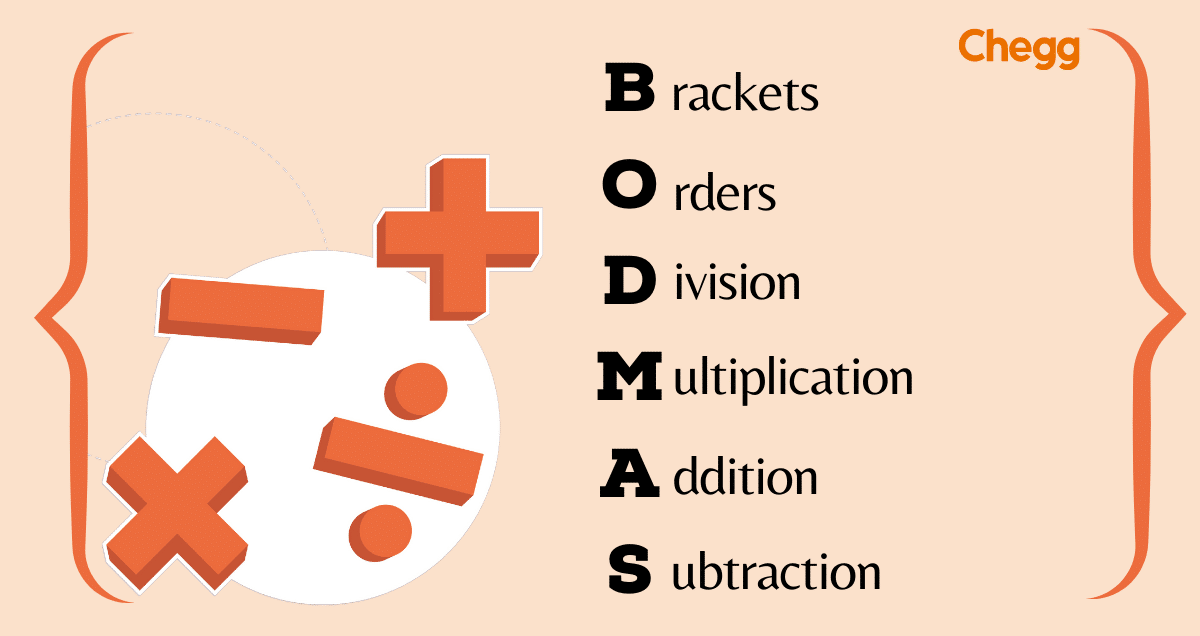
Table of Contents
Introduction – What is BODMAS full form?
A fundamental rule in mathematics is called BODMAS. BODMAS Full form is Brackets, Orders, Division, Multiplication, Addition, and Subtraction, specifies the proper order of operations to do while evaluating mathematical equations. Mathematicians and students can guarantee precise and consistent computations following the BODMAS rule. Look closer at BODMAS’s elements and their role in mathematical operations.
What does BODMAS stand for?
The abbreviation BODMAS stands for the series of steps that should be taken to simplify or solve mathematical statements. In BODMAS, each letter stands for a particular operation:
- Brackets
Brackets, including parentheses, square brackets, or curly braces, are used to group numbers or expressions. They indicate that the enclosed portion should be evaluated as a single entity before proceeding with the rest of the expression.
- Orders
Orders refer to exponents or powers. In mathematical operations, numbers raised to the power or exponent are given precedence and should be calculated before other operations.
- Division and Multiplication
Division and multiplication are performed from left to right in the order they appear in the expression. These operations are given equal precedence and should be executed before addition and subtraction.
- Addition and Subtraction
Addition and subtraction, like division and multiplication, are performed from left to right. These operations are executed after completing brackets, orders, division, and multiplication.
Breakdown of BODMAS components
- Brackets
Calculations can be made simpler using brackets. They aid in determining which components of a statement must be examined first. Mathematicians can reduce complex equations and continue with additional computations by resolving the information contained within the brackets.
- Orders
Dealing with exponents and powers is a part of orders. Exponents show how often a base number has been multiplied by itself. Mathematicians can effectively manage numbers raised to powers by performing exponentiation operations according to the BODMAS formula.
- Division and Multiplication
In mathematics, division, and multiplication are basic operations. The BODMAS rule strongly emphasises carrying out these procedures in the proper sequence, from left to right. Confusion in complex expressions is avoided by following this order, guaranteeing correct and consistent outcomes.
- Addition and Subtraction
The BODMAS formula’s last operations are addition and subtraction. Mathematicians can conduct addition and subtraction progressively to arrive at the ultimate result once brackets, ordering, division, and multiplication have been resolved.
BODMAS rule examples with BODMAS questions with answers
Let’s look at some step-by-step BODMAS rule examples to understand better how it might be used in real-world situations. Consider the following BODMAS question with answers:
- 6 + 3 (8 – 2) 4. Using BODMAS, we evaluate the brackets:
- 8 – 2 = 6.
- After that, we divide 6 by 4 to get 1.5.
- Ultimately, we multiply and add 3 x 6 = 18 and 6 x 18 = 24.
- As a consequence, the phrase produces the number 24.
BODMAS allows us to efficiently answer complex mathematical equations, providing precise results and consistency between calculations.
BODMAS and Problem-Solving
The BODMAS rule extends beyond simplifying expressions. When faced with word problems or mathematical puzzles, applying BODMAS enables us to break down the problem into manageable parts. By identifying the order of operations, we can solve problems systematically and arrive at the correct solutions. Trying BODMAS enhances our mathematical reasoning and problem-solving skills.
Importance of BODMAS in Mathematics
BODMAS is incredibly significant since it removes uncertainty and guarantees accurate results. Adhering to BODMAS becomes crucial in equations and higher-level mathematical ideas. It gives mathematicians, physicists, and engineers a standardized method, enabling them to carry out precise calculations and examine intricate mathematical models.
BODMAS in Real-World Applications
BODMAS finds applications in various fields; let us look at them.
- Engineering
Engineers extensively use BODMAS in complex structural analysis, electrical circuit design, and fluid dynamics calculations.
- Finance and Accounting
Financial professionals rely on BODMAS to calculate compound interest and investment returns and perform accurate financial modelling.
- Computer Science
BODMAS is vital in programming and algorithm design, where mathematical operations are fundamental.
- Physics
Physicists employ BODMAS when solving energy, motion, and quantum mechanics equations.
Conclusion
Understanding the BODMAS Full form and the BODMAS formula is essential for accurate and consistent mathematical computations. By considering the components of BODMAS, including brackets, orders, division, multiplication, addition, and subtraction, mathematicians, and students can simplify expressions, solve complex problems, and enhance their problem-solving skills. Try the BODMAS as a fundamental tool in your mathematical journey to ensure precise and reliable results.
| LPG full form | GMT full form |
| LIC full form | SDM full form |
| SUV full form | CPI full form |
| PFMS full form | IMDb full form |
| SC full form | PRO full form |
BODMAS Full Form: FAQs
BODMAS stands for Brackets, Orders, Division, Multiplication, Addition, and Subtraction.
BODMAS is important as it provides a standardised order of operations, ensuring consistent and accurate calculations.
Yes, the BODMAS rule can be applied to simplify and evaluate all types of mathematical expressions.
While variations exist in different countries and mathematical curricula, the underlying principles of BODMAS remain the same.
No, the order of operations in BODMAS sums should be followed precisely to obtain correct results.
While the order of operations is widely accepted and followed, the acronym BODMAS may vary across different regions. In some countries, it is referred to as PEMDAS (Parentheses, Exponents, Multiplication, Division, Addition, Subtraction) or other similar variations. However, the underlying principles remain the same.
Got a question on this topic?