









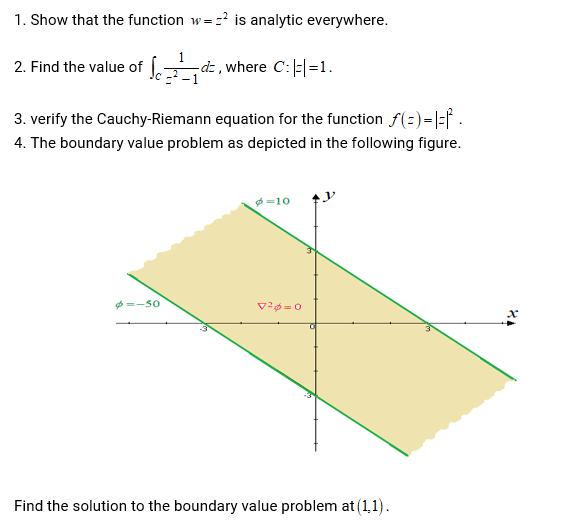



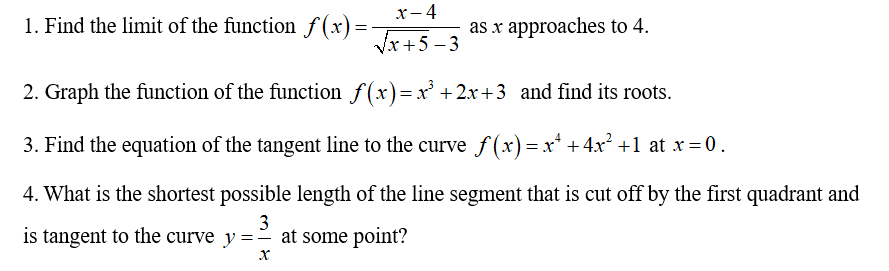







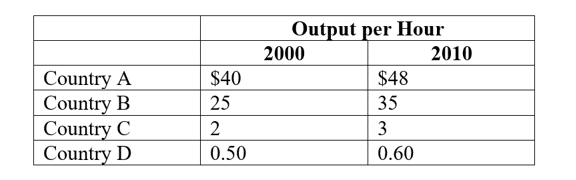
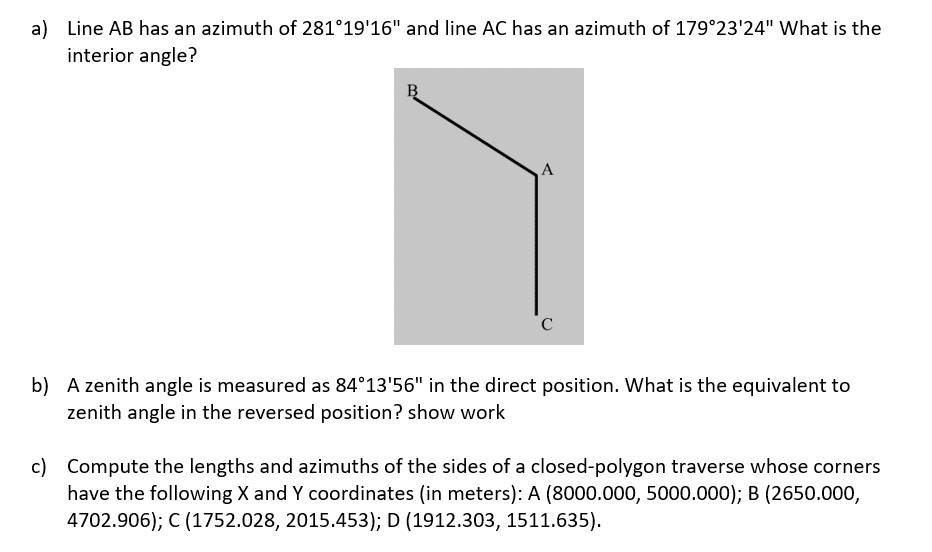
 Instruction: Prepare the following reports: Purchases Journal, Cash Disbursements Journal, and a General Ledger.
Instruction: Prepare the following reports: Purchases Journal, Cash Disbursements Journal, and a General Ledger.








Chegg India does not ask for money to offer any opportunity with the company. We request you to be vigilant before sharing your personal and financial information with any third party. Beware of fraudulent activities claiming affiliation with our company and promising monetary rewards or benefits. Chegg India shall not be responsible for any losses resulting from such activities.
Chegg India does not ask for money to offer any opportunity with the company. We request you to be vigilant before sharing your personal and financial information with any third party. Beware of fraudulent activities claiming affiliation with our company and promising monetary rewards or benefits. Chegg India shall not be responsible for any losses resulting from such activities.